Mathalaxie – DiA:GO – Python trifft Pythagoras

Wie im letzten Beitrag angekündigt, werde ich immer mal wieder über Entwicklungen in der Mathematikdidaktik berichten. Schön, dass es aktuell so viel über neue Erkenntnisse zu berichten gibt. Darum soll es hier gehen. Und auch um Tipps, wie man vor allem stärkeren Schüler*innen gerecht werden kann. Denn auch diese Gruppe hat ein Recht auf Förderung, oder?

Dazu ganz zu Beginn eine didaktische Idee, der ich letzte Woche begegnet bin: Die Seminarmethode ^[1]https://www.cultofpedagogy.com/classroom-seminars/.

Grundsätzlich sind Seminare Kleingruppenunterricht. Meehan erläutert in einem Podcast, dass sie die Bezeichnung Seminar ganz bewusst gewählt habe, eben weil die Kinder es lieben. Die Seminare dauern sieben bis zehn Minuten, wobei jedes Seminar ein kleines, fokussiertes Thema abdeckt. Sie werden in Zeiten angeboten, in denen die Lernenden selbstständig an Aufgaben arbeiten. Während einer Unterrichtsstunde (45-60 Minuten) bietet Meehan normalerweise ein oder zwei Seminare an. Grundsätzlich kann dieses Format in allen Fächern angeboten werden: Das können beliebige Lernziele sein, die die Einheit verfolgt. Es können Aufgaben sein, die sich aus Rückmeldungen der Lernenden ergeben. Idealerweise, so Meehan, werden Seminare für Gruppen von vier bis fünf Schüler*innen angeboten. Wenn sich mehr für ein Seminar anmelden, werden zwei separate Sitzungen angeboten. Oder, wenn viele Lernenden Interesse an einem Thema zeigen, entwickelt sie einen Organisationsrahmen gleich für die ganze Klasse.

Viele Didakter*innen machen sich Gedanken, wie sie das Mathe-ist-doof Image auflösen können. Wie man Schüler*innen für die Mathematik begeistern kann. Darum wird es nun im Folgenden gehen. Die erste Anregung habe ich einer Sendung des SWR2 entnommen ^[2] … Continue reading:

Die Ungarin Marta Vitalis stellte sich schon früh die Frage: Wie sollte man Mathematik vermitteln, sodass es Kindern Spaß macht, ganz ohne Angst? Ihre Antwort: Verpackt in einer Abenteuergeschichte.

Das Spiel “Mathalaxie” verpackt Grundschul-Mathematik in eine Abenteuerreise in den Weltraum. Die Idee: Die Kinder wollen ein Alien besuchen. An zehn Stationen bereiten sie sich auf die abenteuerliche Reise vor und lösen jede Menge Aufgaben: Sie bauen einen Roboter und ein Raumschiff, berechnen Flugrouten, basteln, zeichnen, schrauben. Dass viele Aufgaben mit Mathematik zu tun haben, merken sie nicht. Das sei der große Unterschied zum Unterricht, sagt Marta Vitalis. Denn hier haben sie bei jeder Aufgabe ein klares Ziel vor Augen.

Aus der Forschung weiß man mittlerweile, dass gerade Kinder im angeleiteten Spiel genauso gut lernen wie im traditionellen Unterricht. Bei “Mathalaxie” arbeiten sie außerdem in Gruppen, sind emotional dabei und motiviert – auch das sind Faktoren, die dem Lernen guttun. Sie erleben eine rundum positive Mathe-Erfahrung. Momentan arbeiten Marta Vitalis und zwei Kollegen an “Mastory”, einem Algebra-Kurs für die 8. und 9. Klasse an Highschools in den USA.

Der nächste Vorschlag stammt von einer Forschungsgruppe in Tübingen. Sie haben sich überlegt, wie digitale Medien den Matheunterricht unterstützen können. Herausgekommen sind aktuell drei Lernumgebungen ^[3]https://eldorado.tu-dortmund.de/bitstream/2003/40440/1/BzMU21_PLICHT_AdaptiverUnterricht.pdf:

Was ist das überhaupt, eine adaptive Lernumgebung?

Adaptiv gestaltete Lernräume bieten gerade in heterogenen Lerngruppen besondere Potenziale Unterrichtsprozesse so zu realisieren, dass die aktuellen Unterrichtsinhalte und -methoden an die Voraussetzungen der Schülerinnen und Schüler angepasst sind. Zentrale Bestandteile adaptiven Unterrichts ist die Adaption auf Makro- (z. B. Gruppendifferenzierung nach Leistungsniveau) und Mikroebene (z. B. individuelle Unterstützungsmaßnamen), als auch die formative Diagnose. Eine regelmäßige Diagnostik ist Voraussetzung, um die Lernmaterialien und das Unterrichtsgeschehen fortwährend sowohl auf Makro- als auch auf Mikroebene anzupassen. Formative Diagnose als auch angepasste Adaptionen werden als wichtige Methoden angesehen, um das individuelle Lernen der SchülerInnen gezielt zu fördern, wie auch ihre metakognitiven Selbsteinschätzungen zu unterstützen, welche eine zentrale Rolle im Lernprozess spielen. Digitale Medien dienen hierbei als didaktische Werkzeuge, um diese Unterrichtsprozesse zu realisieren. Sie können sowohl auf Mikroebene für instruktionale Unterstützungsmaßnahmen wie z. B. computergestütztes Feedback als auch auf der Makroebene zur Organisation und Bereitstellung von differenziertem Unterrichtsmaterial eingesetzt werden. Zudem können Audience Response Systeme oder Online-Quizze für eine formative Diagnose mit unmittelbarer Ergebnisauswertung verwendet werden (vgl. hierzu meine Themenseite).

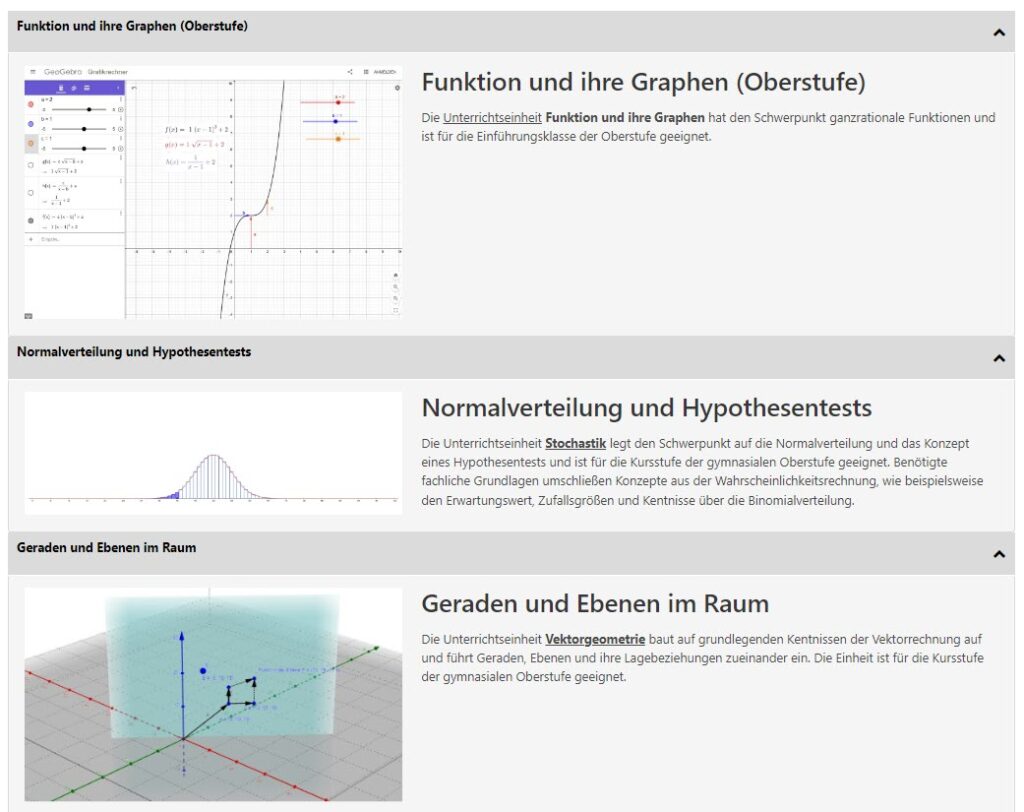
Das Projekt DiA:GO (Digitale Medien im adaptiven Unterricht der gymnasialen Oberstufe der Gemeinschaftsschule) ist ein Kooperationsprojekt der Eberhard Karls Universität Tübingen und der Gemeinschaftsschule West Tübingen, welches auf die Etablierung eines didaktisch sinnvollen Einsatzes digitaler Medien im adaptiven Unterricht abzielt. Im bisherigen Projektzeitraum wurden drei Unterrichtseinheiten für das Fach Mathematik in der Sekundarstufe II entwickelt, durchgeführt und evaluiert (mit Klick auf das Bild kommt man zu den Materialien):

Die Ergebnisse zeigten einen Leistungszuwachs der Schülerinnen und Schüler (große Effekte). Die Schülerinnen und Schüler bewerteten die Unterrichtseinheiten über die Durchführungsphase hinweg gleichbleibend als hoch adaptiv, kognitiv aktivierend und motivierend. In ihrem Fazit schreiben die drei Forscher*innen:

Die Unterrichtseinheiten zeigen einen tragfähigen Ansatz auf, um digitale Medien für die Orchestrierung adaptiver Unterrichtsinhalte bereitzustellen, da sowohl die Lernleistungen als auch Selbstregulationsprozesse innerhalb der Unterrichtseinheit gefördert wurden.

Abschließend und einen Bogen zur eingangs vorgestellten Seminaridee spannend gehe ich auf ein Buch ein, das den stärkeren Lernenden der Sekundarstufe I und II zusätzliche Impulse geben kann:

Auch wenn Computerbeweise bei einigen Mathematiker*innen umstritten sein mögen, sind sie heute nicht mehr wegzudenken. Bedeutende mathematische Beweise, die durch interaktive Theorembeweiser überprüft wurden, sind der Beweis des Vier-Farben-Satzes durch Georges Gonthier ^[4]https://eldorado.tu-dortmund.de/bitstream/2003/40440/1/BzMU21_PLICHT_AdaptiverUnterricht.pdf sowie der formalisierte Beweis der Keplerschen Vermutung durch das Flyspeck-Projekt. ^[5]https://arxiv.org/abs/1501.02155. Vielfach werden Computer gerne eingesetzt, um Aussagen zu falsifizieren. Denn dann braucht man sich ja erst gar nicht auf die Suche begeben. 

Was liegt näher, als bereits frühzeitig die (starken) Schülerinnen und Schüler die Möglichkeit zu geben, sich in dieses Thema einzuarbeiten?  Die Fähigkeiten, die benötigt werden, um guten, logisch kohärenten Code zu schreiben, ähneln stark dem Wissen, das unsere Lernenden auch zur Lösung mathematischer Probleme brauchen. Sie erfahren nicht nur, wie Probleme elegant mit (hier) Python modelliert werden und welche wissenschaftlichen Zusatzmodule ihnen viel Arbeit abnehmen, sondern sie bauen auch selbst Algorithmen nach und verstehen durch diesen konkreten Ansatz mathematische Zusammenhänge, die sonst abstrakt und kompliziert blieben.

Zunächst wird man im Buch mit der Python-Programmierung vertraut gemacht. Es werden in einem kurzen Python-Kurs wichtige Datentypen und Programmierkonstrukte vermittelt. Und als ein erstes Kennzeichen späterer Erfahrungen im Informatikunterricht: Man lernt Bibliotheken zu nutzen; mit Informationen über NumPy, Matplotlib, SymPy und SciPy.

Im Buch werden Themen angesprochen, die im Seminarsetting (s. o.) von der Lehrkraft angesprochen werden können, um sie dann von den Schüler*innen weiterbearbeiten zu lassen. Viele im Mathematikstudium wichtige Fragestellungen kommen im Unterricht kaum noch vor. Im Buch schon, wie z. B. der Begriff der Stetigkeit (nicht streng wissenschaftlich versteht sich, aber doch noch hinreichend formalisiert), Differenzialgleichungen, Ausgleichsrechnungen, Fraktale, Implementierung von RSA-Algorithmen und vieles mehr. Somit werden vor allem Schüler*innen aus der gymnasialen Oberstufe angesprochen, insbesondere diejenigen, die Informatik belegt haben.

In der Sekundarstufe I bieten sich zumindest der Python-Kurs und erste Übungen an, dem Buch (Sieb des Eratostenes) oder aus dem täglichen Unterrichtsgeschehen entnehmend. Iterationsverfahren gibt es ja genügend: z. B. das Heronverfahren zur Berechnung der Quadratwurzel einer (positiven) Zahl oder das Näherungsverfahren von Archimedes zur Bestimmung der Zahl π. Oder man bedient sich der Rückmeldungen der Schüler*innen, wenn sie selbst auf eine Idee, auf eine Anwendung stoßen und umsetzen wollen. Via eines Seminarformats (s.o.) …

Zu jedem der im Buch angesprochenen Themen findet man im Downloadbereich Codebeispiele sowie Übungen mit kommentierten Lösungen. So können Lehrende wie Lernende alle Beispiele komfortabel ausprobieren, die beschriebenen Lösungswege nachvollziehen und auf eigene Probleme anwenden.

Fazit: Ein Buch, das den laufenden Unterricht ergänzen kann. Ein Buch, das eine erste Kontakaufnahme mit Python ermöglicht; einer Programmiersprache, die dank ihrer Syntax und Lesbarkeit leicht zu erlernen ist und sich sehr vielseitig einsetzen lässt. Besonders zu empfehlen für fächerübergreifende Ansätze, indem man z. B. den Begriff des Algorithmus innermathematisch einführt und anschließend im MINT-Spektrum nach weiteren Anwendungsmöglichkeiten sucht.

Wer meinen Beiträgen folgt, weiß um meine Affinität zur evidenzbasierten Bildungsforschung. Auch, weil vor allem die Mathematikdidakter*innen in ihren Beiträgen immer mit Ideen aufwarten, wie man in der Praxis mit den Ergebnissen umgehen kann, wie man z. B. der Inhomogenität in unseren Lerngruppen gerecht werden kann. Und: Weil die Ergebnisse helfen, Erfahrungen aus dem eigenen Unterricht besser einzuordnen. Nicht frustriert zu sein, wenn ^[6]https://www.waxmann.com/index.php?eID=download&buchnr=4257, S. 23 ff

Differenzierungsmaßnahmen nicht immer für alle Schülergruppen mit unterschiedlichen Leistungsniveaus gleich wirksam sind und Merkmale der Schule (z. B. durchschnittlicher sozioökonomischer Status oder Leistung der Schülerinnen und Schüler) entscheidend sein können.

(…)

(Gleichwohl zeigt) die Forschungssynthese mit ihrer vergleichenden Untersuchung von Differenzierungsmaßnahmen auf internationaler Ebene: Es ist Erfolg versprechend, verstärkte Anstrengungen zu unternehmen, um Schülerinnen und Schülern Möglichkeiten zu eröffnen, sich im Regelunterricht in ihrer je eigenen Geschwindigkeit und entsprechend ihren individuellen Fähigkeiten Wissen anzueignen und Fähigkeiten zu erlernen. Hierbei sollte jedoch folgender Grundsatz beachtet werden, welcher auch von einer Lehrkraft mit viel Erfahrung im Bereich Förderung leistungsstarker Schülerinnen und Schüler genannt wurde:

„Es ist ja auch nicht jeder Schüler für jede Maßnahme geeignet. Also, da muss man dann schon immer individuell gucken, was passt.“

Abschließend will ich gerne aus dem zitierten Themenheft die abschließenden Reflexionsfragen (S. 25) empfehlen, eben weil die empirischen Befunde an den jeweiligen Kontext angepasst werden müssen.

… Stay tuned …

Bildnachweis: Gert Altmann @pixabay