Das neue Schuljahr beginnt. Mit neuen und alten Lerngruppen. Mit bewährten und unbekannten, den Unterricht neu belebenden Inhalten und Methoden. Ich werde in loser Folge praxisnahe Ideen aus der Didaktik des MINT-Unterrichts vorstellen. Auch um Anregungen zur Motivation von Schülerinnen und Schüler zu geben, um ein im folgenden Tweet beschriebenes Desinteresse abbauen zu helfen.
Bei meinen S* erlebe ich immer wieder ein großes Desinteresse an der Anwendbarkeit von #Mathematik. Ist das eine von Gott gegebene Eigenschaft, oder ist das tradiertes Desinteresse an der Umwelt? #twlz
— Not N. Druck (@notendruck) July 31, 2021
Mit einer Empfehlung aus der analogen Welt (aka Buchrezension) starte ich heute die Reihe „Matheunterricht interessant gestalten“. Es geht um das Buch DIE WICHTIGSTEN ZAHLEN UND IHRE GESCHICHTEN von Prof. Beutelspacher.
Der C.-H. Verlag bewirbt das Buch so:
Vor mehr als 20000 Jahren aus praktischen Gründen erfunden, haben Zahlen für viele etwas Magisches. Albrecht Beutelspacher erzählt die spannendsten Geschichten rund um die wichtigsten Zahlen. Ein Buch, das sich ganz ohne mathematische Vorkenntnisse erschließt und in dem jeder seine Lieblingszahl entdecken wird.
Über 30 Prozent aller Zahlen beginnen mit 1, und so steht auch die Zahl, mit der das Zählen beginnt, am Ausgangspunkt dieser kurzweiligen Reise durch die Welt der Zahlen. Mit der 2 zerfällt die Welt in zwei Teile, in der 3 wächst sie wieder zusammen. Die 4 ist die Zahl der Orientierung, die 5 die Zahl der Natur und mit der 6 kommt endlich Ordnung in die Welt. Die 7 Weisen waren eigentlich 22, und dafür, dass die Woche ausgerechnet 7 Tage hat, gibt es keine rationalen Gründe. Die 0 hat lange Zeit gefehlt und war, als sie vor 2000 Jahren in Indien erfunden wurde, längst überfällig. Wäre es nach der Französischen Revolution gegangen, hätte ein Tag heute 10 Stunden mit jeweils 100 Minuten, von denen jede aus 100 Sekunden bestünde. Die wilde 13 zerstört die perfekte innere Balance der 12 – muss sie aber deshalb gleich Unglück bringen? Die 5 607 249 ist die größte Zahl, auf die je ein Mensch gezählt hat, aber nicht die größte in diesem Buch. Mit der Kreiszahl p betreten wir das Reich der transzendenten, mit der –1 das Reich der negativen Zahlen. Deren scheinbare Paradoxien illustriert vortrefflich der folgende Witz, der sich ebenfalls in diesem wunderbar leichtfüßig geschriebenen Buch findet: Ein Professor steht vor einem Hörsaal. Er sieht fünf Studierende den Hörsaal betreten und nach einiger Zeit sechs Studierende herauskommen. Da denkt sich der Prof: „Wenn jetzt noch einer reingeht, ist der Hörsaal wieder leer.
Zur Didaktik ...
Lassen Sie mich Ihnen erst einmal den Autor vorstellen. Meinen ersten Kontakt mit dem Hochschulprofessor für Geometrie und Diskrete Mathematik bekam ich durch den Artikel im Licht im Zahlendschungel im SPIEGEL (2004). Als hessische Lehrkraft, noch dazu in der Nähe Gießens arbeitend, nutzte ich mehrfach die Gelegenheit, mit meinen Schülerinnen und Schülern „sein“ Museum zu besuchen. Oder als hessischer Fortbildner sein Angebot zu nutzen, unterrichtende Mathematiklehrkräfte experimentelle Ideen zum MU weiterzugeben, stets verbunden mit einer konkreten Vermittlung seiner vielen Praxismodelle im Museum. Wer seinem didaktischen Verständnis nachspüren möchte, dem empfehle ich:
Beutelspacher hatte noch etwas im Blick: Die Beschäftigung mit der Angst vor dem MU. Das Buch greift die Ansätze aus diesem Artikel auf. Man glaubt gar nicht, welche Geschichten sich hinter den Zahlen 1,2,3, … verbergen. Der Autor nimmt die Leserinnen und Leser, ob jung oder alt mit in die zeithistorische Reise von 500 v. Chr. bis heute. Einfach beeindruckend, wie viel Mathematik sich in Geschichte, Musik, Kunst, Geografie u. v. m. wiederfindet. Was die Akzeptanz dieses Buches deutlich erleichtert, ist die Aufteilung in viele, viele kleine Häppchen. Sehr leicht verdaulich, 
weil eben im Großen und Ganzen auch von „Otto Normal Verbraucher“ verständlich geschrieben, wie einige Pressestimmen bestätigen. Die Schülerinnen und Schüler profitieren darüber hinaus, weil ihnen eine Ahnung vermittelt wird, was sich hinter der Wissenschaft Mathematik so alles verbirgt. Denn Beutelspacher beschreibt Phänomene, mathematische Modelle (Axiomatik, Geometrie, Analysis) und macht – mit Blick auf digitale Technologien – an geeigneten Stellen darauf aufmerksam, dass erst diese Werkzeuge die „Wahrheit“ (aka den Beweis) einiger mathematischen Vermutungen erbracht haben.
... und Methodik I ...
Wir Lehrkräfte können mehrfach Gewinn aus dem Buch ziehen:
Die Anregungen aus seinen Fortbildungen habe ich z. B. immer gerne bei der Einführung eines im Unterricht zu behandelnden Mathe- Themas genutzt. Meine Schülerinnen und Schüler haben mir – selten genug – immer dann 100 % Aufmerksamkeit geschenkt, wenn ich kulturhistorische Bezüge hergestellt habe, wenn ich mit Experimenten begonnen habe, wenn ich plötzlich mit einem Musikstück die Unterrichtseinheit begonnen habe, etwa bei der Einführung der Zahl π: Ich kam in die Klasse und spielte ihnen einen Titel von Kate Bush vor, verbunden mit der Frage: „Was hat diese Musikerin möglicherweise motiviert, dieses Lied zu kreieren?“
Der Text und – für mich – die Musik gibt möglicherweise Auskunft: Die Unendlichkeit der Ziffernfolge… Ich reicherte das Ganze noch an mit historischen Hinweisen, wie eben im Buch von Beutelspacher im gleichnamigen Kapitel beschrieben. Und, ganz aktuell bietet sich zu diesem Thema auch ein Bezug zur Forschung an:
Mit 62,8 Billionen Stellen hinter dem Komma haben Schweizer Forscher die Kreiszahl #Pi so genau berechnet wie nie zuvor. Der Rekord lag vorher bei gerade mal 12,8 Billionen Nachkommastellen, teilte die Fachhochschule Graubünden mit.https://t.co/7mP4SmuWTx
— RND (@RND_de) August 23, 2021
Wer WELT Abonnent ist, kann hier ein Interview mit der Leiter der Schweizer Forschungsgruppe finden. Schülerinnen und Schüler fallen eine ganze Reihe von Fragen ein. Auch die, wozu das gut sein soll. Und schon war der Advance Organizer, einer meiner bevorzugten Initiierungsmethode für die Unterrichtseinheit fertig. Denn darum geht uns Lehrkräften doch: Zum Nachdenken anregen, Schülerinnen und Schüler zu motivieren, sich mal selbst auf den Weg zu machen. Übrigens bieten sich für einen fächerübergreifenden Ansatz Querverbindungen zu den Fächern Englisch/ Deutsch (Thema Lyrik) an.
... und Methodik II
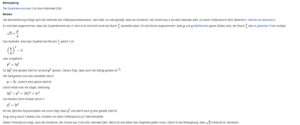
Auch bei den vom Autor vorgestellten Beweistechniken können Lehrkräfte profitieren: Ich habe meine Schülerinnen und Schüler stets „verloren“, wenn es um Widerspruchsbeweise, vollständige Induktion und weitere Beweisstrategien ging. Hier ein Beispiel, von dem ich glaube, dass der Begleittext von Beutelspacher möglicherweise ein besseres Verständnis befördern hilft. Es geht um den Widerspruchsbeweis zu „√2 ist nicht rational“. Die Schulbuchvarianten ähneln der Wikipediaversion (siehe unten links), die ich nun der Beutelspacher- Variante gegenüberstelle. Fragen Sie einmal Ihre Schülerinnen und Schüler, welche der beiden Varianten besser „verstanden“ wird (zur Vergrößerung einfach anklicken). Meine Vermutung, die textlastigere rechte Variante:
Schlussbemerkung
Zusammenfassend kann es für dieses kleine handliche Bändchen nur eine klare Empfehlung geben: Für unseren Matheunterricht, für unsere Schülerinnen und Schüler, wie auch für all die Zeitgenossen, die immer wieder mit dem Spruch „In Mathe war ich auch immer schlecht.” aufwarten. Wie wäre es mit einer ergänzenden Aussage, die ich kürzlich in meinem Bekanntenkreis gehört habe: „Hätte ich dieses Buch gekannt, hätte ich vielleicht eine Chance gehabt, aus dem Matheunterricht mehr mitzunehmen …”
Und, wer Geschmack gefunden hat: Der DLF hat in einem Podcast mit dem Titel Wie Mathematik unser Leben prägt zwei spannende Sachbücher vorgestellt. Gerne mal reinhören …
In diesem Sinne
Stay tuned
Bildnachweis:
Titel- bzw. Coverbild: @C. H. Beck- Verlag
Beweistechnik, links: @Wikipedia
Beweistechnik, rechts: @Beutelspacher: Auszug aus vorgestelltem Buch, S. 136